The HeuristicCubicSpectrumModel class is a data model to represent an (heuristic) X-ray spectrum with respect to a simple degree-three polynomial. More...

#include <xrayspectrummodels.h>

Inheritance diagram for CTL::HeuristicCubicSpectrumModel:

[legend]

Collaboration diagram for CTL::HeuristicCubicSpectrumModel:

[legend]

Public Types
enum	{ Type = 42 }

Public Types inherited from CTL::AbstractDataModel
enum	{ Type = 0 }

Public Types inherited from CTL::SerializationInterface
enum	{ Type = -1, UserType = 65536 }

Public Member Functions
int	type () const override

float	valueAt (float position) const override
	Returns the value (i.e. photon count per energy) of the model at the given position (in keV). More...

float	binIntegral (float position, float binWidth) const override
	Returns the integral over model values (i.e. total number of photons) in the (energy) interval [position - 0.5 * binWidth, position + 0.5 * binWidth]. More...

HeuristicCubicSpectrumModel *	clone () const override

Public Member Functions inherited from CTL::AbstractXraySpectrumModel
void	setParameter (const QVariant &parameter) override
	Sets the energy parameter to parameter. More...

QVariant	parameter () const override

Public Member Functions inherited from CTL::AbstractIntegrableDataModel
float	meanValue (float position, float binWidth) const

Public Member Functions inherited from CTL::AbstractDataModel
void	fromVariant (const QVariant &variant) override

QVariant	toVariant () const override

bool	isIntegrable () const

void	setName (const QString &name)

const QString &	name () const

Public Member Functions inherited from CTL::SerializationInterface
virtual	~SerializationInterface ()=default

Friends
template<class >
struct	SerializationHelper::RegisterWithSerializationHelper

Additional Inherited Members
Protected Member Functions inherited from CTL::AbstractIntegrableDataModel
	AbstractIntegrableDataModel (const AbstractIntegrableDataModel &)=default

	AbstractIntegrableDataModel (AbstractIntegrableDataModel &&)=default

AbstractIntegrableDataModel &	operator= (const AbstractIntegrableDataModel &)=default

AbstractIntegrableDataModel &	operator= (AbstractIntegrableDataModel &&)=default

Protected Member Functions inherited from CTL::AbstractDataModel
	AbstractDataModel (const AbstractDataModel &)=default

	AbstractDataModel (AbstractDataModel &&)=default

AbstractDataModel &	operator= (const AbstractDataModel &)=default

AbstractDataModel &	operator= (AbstractDataModel &&)=default

Protected Member Functions inherited from CTL::SerializationInterface
	SerializationInterface ()=default

	SerializationInterface (const SerializationInterface &)=default

	SerializationInterface (SerializationInterface &&)=default

SerializationInterface &	operator= (const SerializationInterface &)=default

SerializationInterface &	operator= (SerializationInterface &&)=default

Protected Attributes inherited from CTL::AbstractXraySpectrumModel
float	_energy = 0.0f
	Control parameter of device setting (usually tube voltage).

Related Functions inherited from CTL::AbstractDataModel
	DataModelPtr
	Template alias name for CopyableUniquePtr<ModelType> to a suitable ModelType.

	AbstractDataModelPtr
	Alias name for DataModelPtr<AbstractDataModel>. More...

std::unique_ptr< ModelType >	makeDataModel (ConstructorArguments &&... arguments)

using DataModelPtr	CopyableUniquePtr
	Alias name for CopyableUniquePtr<ModelType> to a suitable ModelType.

Detailed Description

The HeuristicCubicSpectrumModel class is a data model to represent an (heuristic) X-ray spectrum with respect to a simple degree-three polynomial.

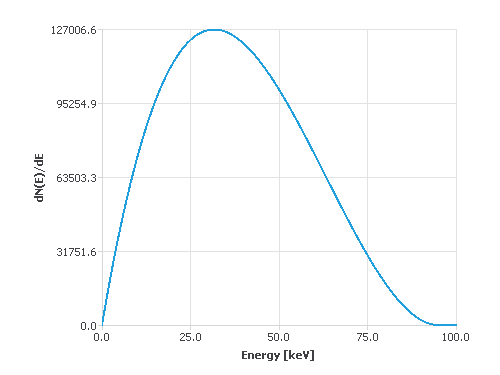
This class uses a simple cubic polynomial to (roughly) approximate the shape of a real X-ray spectrum. Different from KramersLawSpectrumModel, this also includes the effect that the number of emitted photons drops towards low energies.

For details on the model, see valueAt() and binIntegral().

Example:

HeuristicCubicSpectrumModel model;
model.setParameter(95.0f);
// sample the model in the interval [0, 100] keV and visualize the model
// Note: visualization requires the 'gui_widgets_charts.pri' submodule
gui::plot(XYDataSeries::sampledFromModel(model, 0.0f, 100.0f, 100),
          "Energy [keV]", "dN(E)/dE");

Visualization of a HeuristicCubicSpectrumModel at energy parameter 95 keV.

Member Function Documentation

◆ binIntegral()

float CTL::HeuristicCubicSpectrumModel::binIntegral	(	float	position,
		float	binWidth
	)		const

overridevirtual

Returns the integral over model values (i.e. total number of photons) in the (energy) interval [position - 0.5 * binWidth, position + 0.5 * binWidth].

Let \( E_{max} \) be the currently set energy parameter of this instance and \( [E_0, E_1] \) the borders of the bin as specified by position and binWidth, then the bin integral can be expressed as follows:

\( \begin{align*} N &= \int_{E_0^{*}}^{E_1^{*}} \frac{dN(E)}{dE} \,dE = \left[ -\frac{1}{3}E_{max} (E_{max} - E)^3 +\frac{1}{4} (E_{max} - E)^4 \right]_{E_0^{*}}^{E_1^{*}} \end{align*} \)

Note that \( E_0^{*} \) and \( E_1^{*} \) are modified boundaries as follows:

\( \begin{align*} E_0^{*} &= \max(E_0, 0) \\ E_1^{*} &= \min(E_1, E_{max}) \end{align*} \)

Note that the scaling factor of these values is arbitrary and in practical cases (e.g. when used in source components of the CTL) the number of photons scales with the irradiated area, the distance from the source and typically another proportionality describing the output power (e.g. tube current).

Implements CTL::AbstractIntegrableDataModel.

◆ clone()

HeuristicCubicSpectrumModel * CTL::HeuristicCubicSpectrumModel::clone ( ) const

overridevirtual

Creates a copy of this instance and returns a base class pointer to the new object.

Implements CTL::AbstractXraySpectrumModel.

◆ type()

int CTL::HeuristicCubicSpectrumModel::type ( ) const

inlineoverridevirtual

Returns the type id of this instance.

Reimplemented from CTL::AbstractDataModel.

◆ valueAt()

float CTL::HeuristicCubicSpectrumModel::valueAt ( float position ) const

overridevirtual

Returns the value (i.e. photon count per energy) of the model at the given position (in keV).

Let \( E_{max} \) be the currently set energy parameter of this instance and \( E \) the requested sampling point (i.e. position), then the underlying function for this model is given by: \( \frac{dN(E)}{dE}= \begin{cases} E_{max} * (E_{max} - E)^2 - (E_{max}- E)^3 & E < E_{max} \\ 0 & E \geq E_{max} \end{cases} \)

Note that the scaling factor of these values is arbitrary and in practical cases (e.g. when used in source components of the CTL) the number of photons scales with the irradiated area, the distance from the source and typically another proportionality describing the output power (e.g. tube current).

Implements CTL::AbstractDataModel.

The documentation for this class was generated from the following files:

modules/src/models/xrayspectrummodels.h
modules/src/models/xrayspectrummodels.cpp

Public Types

Public Member Functions

Friends

Additional Inherited Members

Detailed Description

Member Function Documentation

◆ binIntegral()

◆ clone()

◆ type()

◆ valueAt()